[译]B-Tree叶节点格式

我们将表的格式从未排序的行数组更改为 B 树。这是一个很大的更改，需要多篇文章来实现。在本文的结尾，我们将定义叶节点的布局，并支持将键/值对插入到单节点树中。但首先，让我们回顾一下切换到树结构的原因。

替代表格格式

使用当前格式，每个页面仅存储行（无元数据），因此非常节省空间。插入也很快速，因为我们只需追加到末尾即可。但是，只能通过扫描整个表来查找特定行。如果要删除一行，则必须通过移动其后的每一行来填补该空缺。

如果我们将表存储为数组，但按 id 对行进行排序，则可以使用二分查找来查找特定 id。但是，插入会很慢，因为我们必须移动很多行来腾出空间。

相反，我们使用树结构。树中的每个节点可以包含数量可变的行，因此我们必须在每个节点中存储一些信息来跟踪它包含多少行。此外，所有不存储任何行的内部节点还存在存储开销。作为对更大的数据库文件进行交换，我们获得了快速的插入、删除和查找。

	未排序的行数组	已排序的行数组	节点树
页面包含	仅数据	仅数据	元数据、主键和数据
每页行数	更多的	更多的	更少
插入	O(1)	O(n)	O(log(n))
删除	O(n)	O(n)	O(log(n))
通过id查找	O(n)	O(log(n))	O(log(n))

节点头格式

叶节点和内部节点具有不同的布局。让我们创建一个枚举来跟踪节点类型：

typedef enum { NODE_INTERNAL, NODE_LEAF } NodeType;

每个节点将对应一个页面。内部节点将通过存储存储子节点的页号来指向其子节点。B 树向分页器询问特定页号，并从页面缓存中获取回一个指针。页面按页号顺序一个接一个地存储在数据库文件中。

节点需要在页面的开头存储一些元数据作为头。每个节点将存储其节点类型、是否为根节点以及指向其父节点的指针（以便查找节点的兄弟节点）。我为每个头字段的大小和偏移量定义常量：

/*
 * Common Node Header Layout
 */
const uint32_t NODE_TYPE_SIZE = sizeof(uint8_t);
const uint32_t NODE_TYPE_OFFSET = 0;
const uint32_t IS_ROOT_SIZE = sizeof(uint8_t);
const uint32_t IS_ROOT_OFFSET = NODE_TYPE_SIZE;
const uint32_t PARENT_POINTER_SIZE = sizeof(uint32_t);
const uint32_t PARENT_POINTER_OFFSET = IS_ROOT_OFFSET + IS_ROOT_SIZE;
const uint8_t COMMON_NODE_HEADER_SIZE = NODE_TYPE_SIZE + IS_ROOT_SIZE + PARENT_POINTER_SIZE;

叶节点格式

除了这些常见的头字段外，叶节点还需要存储它们包含多少个“单元格”。单元格是键/值对。

/*
 * Leaf Node Header Layout
 */
const uint32_t LEAF_NODE_NUM_CELLS_SIZE = sizeof(uint32_t);
const uint32_t LEAF_NODE_NUM_CELLS_OFFSET = COMMON_NODE_HEADER_SIZE;
const uint32_t LEAF_NODE_HEADER_SIZE = COMMON_NODE_HEADER_SIZE + LEAF_NODE_NUM_CELLS_SIZE;

叶节点的主体是一个单元格数组。每个单元格都是一个键，后跟一个值（序列化的行）。

/*
 * Leaf Node Body Layout
 */
const uint32_t LEAF_NODE_KEY_SIZE = sizeof(uint32_t);
const uint32_t LEAF_NODE_KEY_OFFSET = 0;
const uint32_t LEAF_NODE_VALUE_SIZE = ROW_SIZE;
const uint32_t LEAF_NODE_VALUE_OFFSET = LEAF_NODE_KEY_OFFSET + LEAF_NODE_KEY_SIZE;
const uint32_t LEAF_NODE_CELL_SIZE = LEAF_NODE_KEY_SIZE + LEAF_NODE_VALUE_SIZE;
const uint32_t LEAF_NODE_SPACE_FOR_CELLS = PAGE_SIZE - LEAF_NODE_HEADER_SIZE;
const uint32_t LEAF_NODE_MAX_CELLS = LEAF_NODE_SPACE_FOR_CELLS / LEAF_NODE_CELL_SIZE;

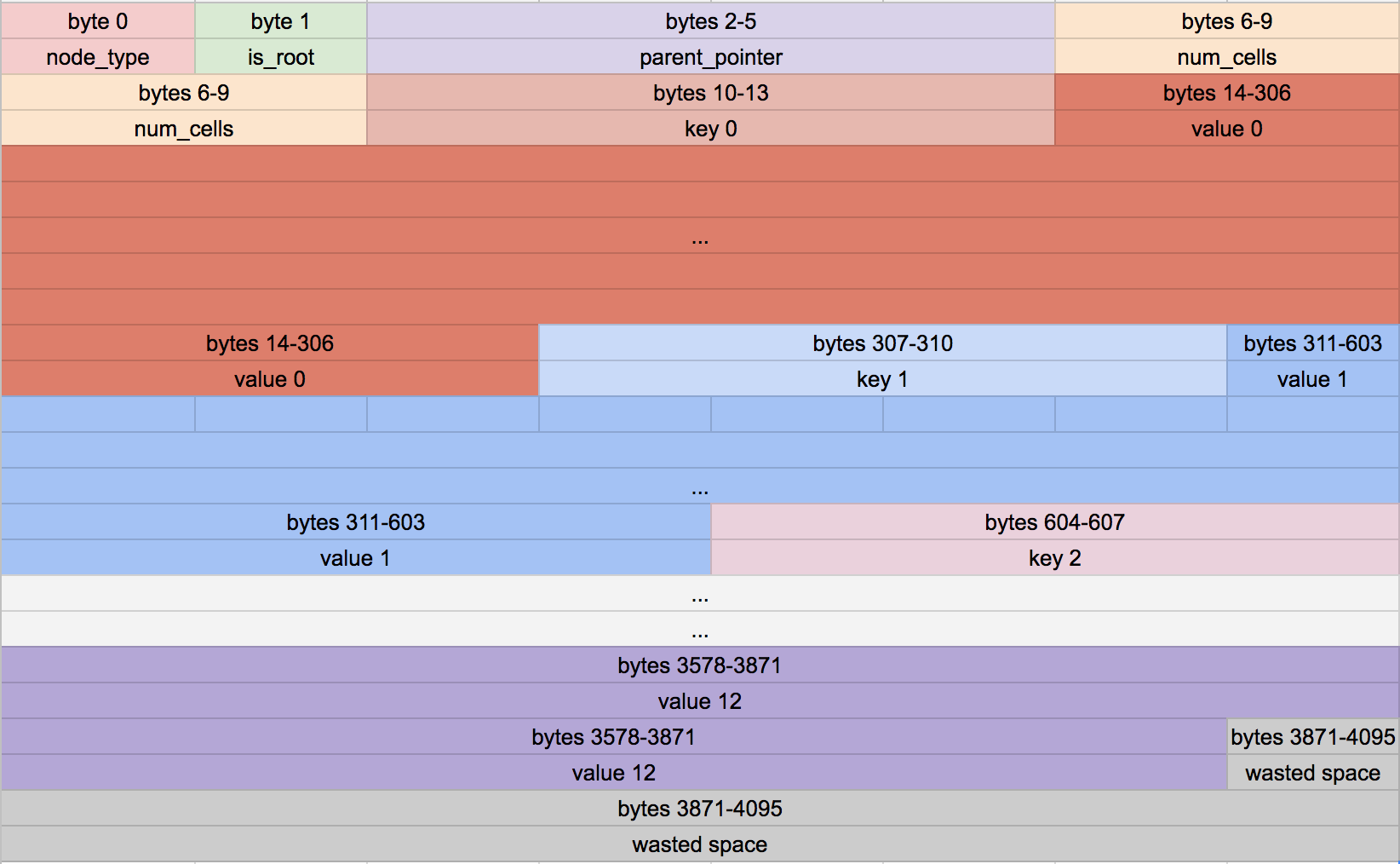
基于这些常量，叶节点的布局当前如下所示：

在标头中每个布尔值使用整个字节的空间效率有点低，但这使得编写代码来访问这些值变得更容易。

另请注意，末尾有一些浪费的空间。我们在标题后存储尽可能多的单元格，但剩余空间无法容纳整个单元格。我们将其留空以避免节点之间的单元格分裂。

访问叶节点字段

访问键、值和元数据的代码都涉及使用我们刚刚定义的常量进行指针算术。

+uint32_t* leaf_node_num_cells(void* node) {
+  return node + LEAF_NODE_NUM_CELLS_OFFSET;
+}
+
+void* leaf_node_cell(void* node, uint32_t cell_num) {
+  return node + LEAF_NODE_HEADER_SIZE + cell_num * LEAF_NODE_CELL_SIZE;
+}
+
+uint32_t* leaf_node_key(void* node, uint32_t cell_num) {
+  return leaf_node_cell(node, cell_num);
+}
+
+void* leaf_node_value(void* node, uint32_t cell_num) {
+  return leaf_node_cell(node, cell_num) + LEAF_NODE_KEY_SIZE;
+}
+
+void initialize_leaf_node(void* node) { *leaf_node_num_cells(node) = 0; }

这些方法返回指向相关值的指针，因此它们既可以用作 getter 也可以用作 setter。

对Pager和表的更改

每个节点都将恰好占用一页，即使它未满。这意味着我们的Pager不再需要支持读/写部分页面。

-void pager_flush(Pager* pager, uint32_t page_num, uint32_t size) {
+void pager_flush(Pager* pager, uint32_t page_num) {
   if (pager->pages[page_num] == NULL) {
     printf("Tried to flush null page\n");
     exit(EXIT_FAILURE);
@@ -242,7 +337,7 @@ void pager_flush(Pager* pager, uint32_t page_num, uint32_t size) {
   }
 
   ssize_t bytes_written =
-      write(pager->file_descriptor, pager->pages[page_num], size);
+      write(pager->file_descriptor, pager->pages[page_num], PAGE_SIZE);
 
   if (bytes_written == -1) {
     printf("Error writing: %d\n", errno);

void db_close(Table* table) {
   Pager* pager = table->pager;
-  uint32_t num_full_pages = table->num_rows / ROWS_PER_PAGE;
 
-  for (uint32_t i = 0; i < num_full_pages; i++) {
+  for (uint32_t i = 0; i < pager->num_pages; i++) {
     if (pager->pages[i] == NULL) {
       continue;
     }
-    pager_flush(pager, i, PAGE_SIZE);
+    pager_flush(pager, i);
     free(pager->pages[i]);
     pager->pages[i] = NULL;
   }
 
-  // There may be a partial page to write to the end of the file
-  // This should not be needed after we switch to a B-tree
-  uint32_t num_additional_rows = table->num_rows % ROWS_PER_PAGE;
-  if (num_additional_rows > 0) {
-    uint32_t page_num = num_full_pages;
-    if (pager->pages[page_num] != NULL) {
-      pager_flush(pager, page_num, num_additional_rows * ROW_SIZE);
-      free(pager->pages[page_num]);
-      pager->pages[page_num] = NULL;
-    }
-  }
-
   int result = close(pager->file_descriptor);
   if (result == -1) {
     printf("Error closing db file.\n");

现在，在数据库中存储页数而不是行数更有意义。页数应该与分页器对象相关联，而不是与表相关联，因为它是数据库使用的页数，而不是特定的表。 B 树由其根节点页码标识，因此表对象需要跟踪它。

 const uint32_t PAGE_SIZE = 4096;
 const uint32_t TABLE_MAX_PAGES = 100;
-const uint32_t ROWS_PER_PAGE = PAGE_SIZE / ROW_SIZE;
-const uint32_t TABLE_MAX_ROWS = ROWS_PER_PAGE * TABLE_MAX_PAGES;
 
 typedef struct {
   int file_descriptor;
   uint32_t file_length;
+  uint32_t num_pages;
   void* pages[TABLE_MAX_PAGES];
 } Pager;
 
 typedef struct {
   Pager* pager;
-  uint32_t num_rows;
+  uint32_t root_page_num;
 } Table;

@@ -127,6 +200,10 @@ void* get_page(Pager* pager, uint32_t page_num) {
     }
 
     pager->pages[page_num] = page;
+
+    if (page_num >= pager->num_pages) {
+      pager->num_pages = page_num + 1;
+    }
   }
 
   return pager->pages[page_num];

@@ -184,6 +269,12 @@ Pager* pager_open(const char* filename) {
   Pager* pager = malloc(sizeof(Pager));
   pager->file_descriptor = fd;
   pager->file_length = file_length;
+  pager->num_pages = (file_length / PAGE_SIZE);
+
+  if (file_length % PAGE_SIZE != 0) {
+    printf("Db file is not a whole number of pages. Corrupt file.\n");
+    exit(EXIT_FAILURE);
+  }
 
   for (uint32_t i = 0; i < TABLE_MAX_PAGES; i++) {
     pager->pages[i] = NULL;

光标对象的更改

光标代表表中的位置。当我们的表是一个简单的行数组时，我们可以仅通过行号来访问行。现在它是一棵树，我们通过节点的页码以及该节点内的单元格编号来标识位置。

 typedef struct {
   Table* table;
-  uint32_t row_num;
+  uint32_t page_num;
+  uint32_t cell_num;
   bool end_of_table;  // Indicates a position one past the last element
 } Cursor;

 Cursor* table_start(Table* table) {
   Cursor* cursor = malloc(sizeof(Cursor));
   cursor->table = table;
-  cursor->row_num = 0;
-  cursor->end_of_table = (table->num_rows == 0);
+  cursor->page_num = table->root_page_num;
+  cursor->cell_num = 0;
+
+  void* root_node = get_page(table->pager, table->root_page_num);
+  uint32_t num_cells = *leaf_node_num_cells(root_node);
+  cursor->end_of_table = (num_cells == 0);
 
   return cursor;
 }

转

https://cstack.github.io/db_tutorial/parts/part8.html